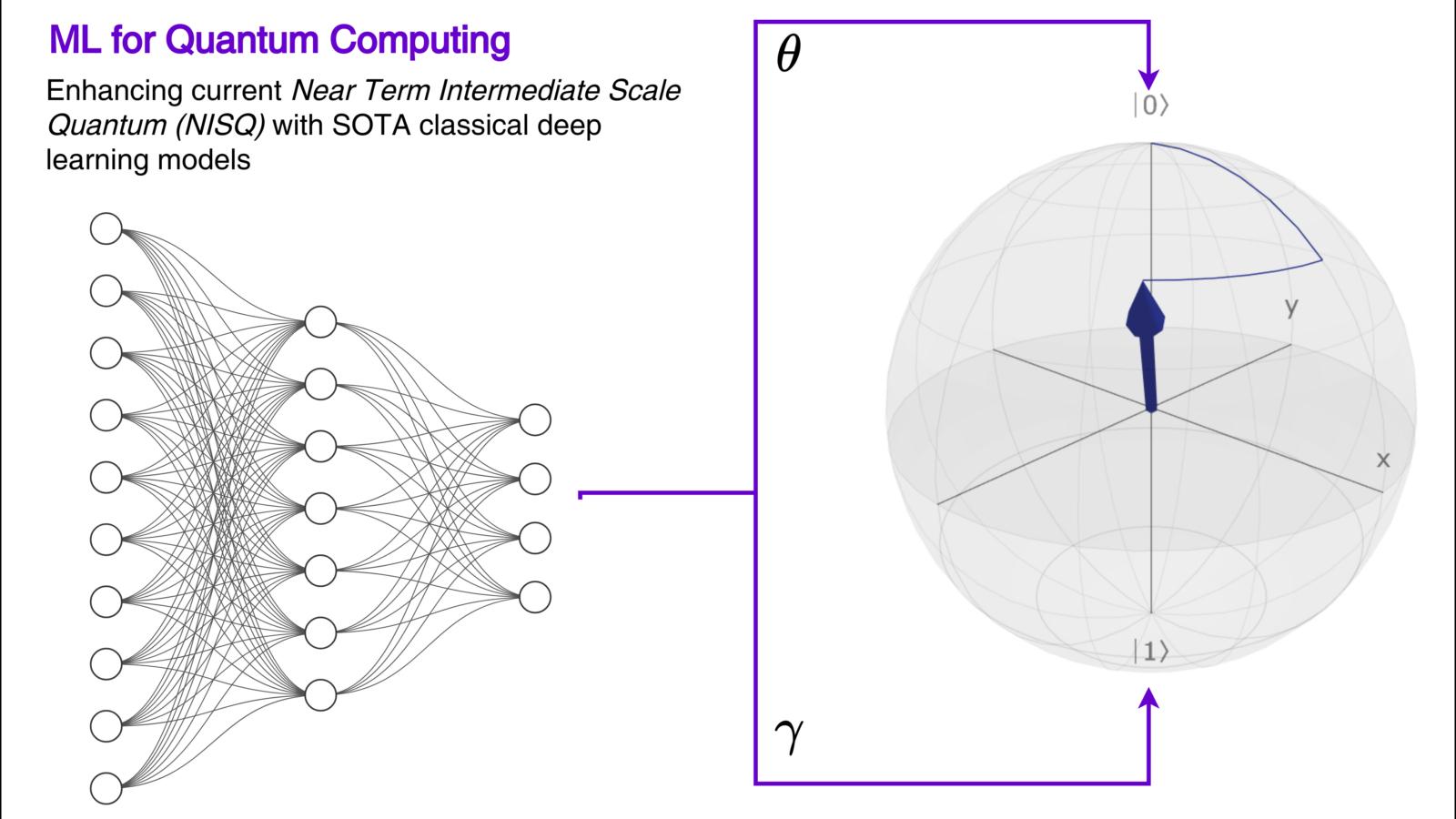
Our Vision
Our research vision is to create a symbiotic partnership between these two transformative technologies, where machine learning optimizes and accelerates quantum hardware development, while quantum computing unleashes new paradigms for machine learning algorithms. We envision ML algorithms not only designing and tailoring quantum circuits for specific tasks, but also actively managing and correcting noise in real-time, enabling a leap in quantum coherence and fidelity.
Resource List
Quantum Computing Resources
I. Reading Resources
- Qiskit Tutorials: The course functions like a practical introduction.
- Quantum Computing and Quantum Information: Quintessential textbook for concepts of Quantum Computing,
- An Introduction to Quantum Computing: A concise, accessible text provides a thorough introduction to quantum computing
- Jack Hidary Quantum Computing Book
II. Course Resources
- UTQML101x: Quantum Machine Learning: Very detailed course with a good balance of theoretical concepts, math, and coding exercises by the university of Toronto,
- IBM Qiskit Summer School: A 3-week program every year with a new area of focus
- A Modern Approach to Quantum Mechanics, Rutgers Course, Lectures, Problems
III. Community Posts
- My Path into Quantum Computing: LinkedIn post for Quantum Computing resources
- Quantum Computing for Students of Computer Science: Intro to Qubit from ML developer perspective
- Quantum Computing Series by Jonathan Hui on Medium
IV. YouTube Resources
- Quantum Mechanics and Quantum Computing: A very early but well-taught course by Prof Umesh Vazirani
- Qiskit Youtube Series
- Quantum Machine Learning MOOC by Peter Wittek from University of Toronto
- Quantum Computing Playlist by Dr. Faisal Aslam
- Quantum Computing by John Preskill
- One good lecture from Microsoft
- Quantum Machine Learning videos from IndabaX
V. Quantum Mechanics
- Quantum Mechanics course from MIT by Allan Adams
- Quantum Physics course from MIT by Barton Zwiebach